- Is there a cycle? use Floyd’s Cycle Detection Algorithm
- Can the problem be broken down into subproblems? use Dynamic Programming
- Is the problem asking for the longest/shortest sequence? use Sliding Window
- Quick lookup for space time complexity of data structures and algorithms: https://www.bigocheatsheet.com/
- Is it of the type, “top k elements”? use Heap
- Is it of the type, “find the shortest path”? use Dijkstra’s Algorithm
- Do you need to search, use Binary Search
Main Concepts
- Strings
- Arrays
- Linked Lists
- Stacks
- Queues
- Trees
- Graphs
- Hash Tables
- Heaps
- Sorting
- Searching
- Dynamic Programming
- Greedy Algorithms
- Backtracking
- Bit Manipulation
- Recursion
- Divide and Conquer
- Sliding Window
- Two Pointers
Floyd’s Cycle Detection Algorithm
Anytime you have a problem that involves detecting a repeating node/number and you can create a cycle for it, think about Floyd’s Cycle Detection Algorithm. It uses two pointers to traverse the linked list. One pointer moves one node at a time, while the other pointer moves two nodes at a time. If the linked list has a cycle, the two pointers will eventually meet. If there is no cycle, the fast pointer will reach the end of the linked list.
Dynamic Programming
Top-down approach (memoization) - start solving the given problem by breaking it down. If you see that the problem has been solved already, then just return the saved answer. If it has not been solved, solve it and save the answer. This is usually easy to think of and very intuitive. This is referred to as the top-down approach since we start from the top (the original problem) and work our way down (towards the base case).
Bottom-up approach (tabulation) - analyze the problem and see the order in which the sub-problems are solved and start solving from the trivial subproblem, up towards the given problem. In this process, it is guaranteed that the subproblems are solved before solving the problem. This is referred to as bottom-up approach since we solve the problem level by level from the bottom (the trivial subproblem) until we reach the top (the required solution).
Sliding Window
Fixed Window - The window size is fixed. The window slides by one element when we move to the next position. The window size remains the same throughout the process.
Variable Window - The window size is not fixed. The window slides by one element when we move to the next position. The window size changes according to the problem.
Binary Search
Keep in mind to replace start with mid + 1 and end with mid - 1 when you want to shrink your search space. That way you will never get stuck in an infinite loop and your solution will be accepted. Also, make sure your mid is calculated as start + (end - start) / 2 to avoid overflow.
Binary Search Template
int binarySearch(vector<int>& nums, int target) {
int left = 0, right = nums.size()-1;
while (left <= right) {
int mid = (left + right) / 2;
if (nums[mid] == target) return mid;
else if (nums[mid] < target) left = mid + 1;
else right = mid - 1;
}
return -1;
}
Trees & Graphs
Tree is a special case of a connected, acyclic, undirected graph.
- BFS: Using a queue
- DFS: Using a stack
- Cycle in Directed Graph: DFS with path visited and visited array
- Cycle in Undirected Graph: DFS with path visited array
- Dijkstra’s Algorithm: Shortest path in a weighted graph with positive weights and no cycles
- Topological Sort
- Minimum Spanning Tree
- Union Find
Edges (E) and Vertices (V)
- For a connected undirected acyclic graph (Tree), E = V - 1.
- Max number of edges in a undirected graph = V * (V - 1)/2
Binary Search Tree
Binary search trees: Directed acyclic graphs with maximum of two children per node and left child is always smaller than the right child.
Inorder traversal of a BST gives a sorted list of elements.
AVL vs Binary Search Tree vs Red Black Tree
Since there is the added overhead of checking and updating balance factors and rotating nodes, insertion and deletion in AVL trees can be pretty slow when compared to non-balanced BST’s.
Because of the tight balancing, search will never take linear-like time, so you’ll probably want to use AVL trees in situations where searching is a more frequent operation than updating the tree.
Red Black Trees are used in most of the language libraries like map, multimap, multiset in C++ whereas AVL trees are used in databases where faster retrievals are required.
AVL trees store balance factors or heights with each node, thus requires storage for an integer per node whereas Red Black Tree requires only 1 bit of information per node.
AVL will consume more memory (each node has to remember its balance factor) and each operation can be slower (because you need to maintain the balance factor and sometimes perform rotations).
BST without balancing has a very bad (linear) worst case. But if you know that this worst case won’t happen to you, or if you’re okay if the operation is slow in rare cases, BST without balancing might be better than AVL.
Dijkstra’s Algorithm
Dijkstra’s algorithm is an algorithm for finding the shortest path between one node and every other node in a weighted graph with positive weights. It uses a min priority queue. Nodes are added to the queue with their distance from the source node. The starting node is added to the queue and its neighbours added. We then remove the node with the smallest distance from the queue and add its neighbours to the queue. We continue this process until we visit all the nodes or the queue is empty. The time complexity is O(E + V log V) where E is the number of edges and V is the number of vertices.
Data Structures
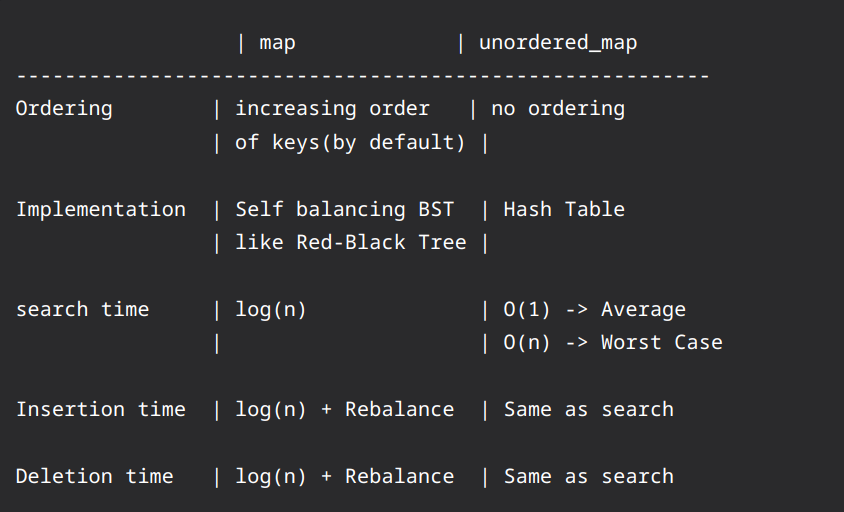
Set (Red Black Tree) vs Unordered Set (Hash Table)
- Set has a time complexity of O(log n) for insertion and lookup operations, while unordered_set has a amortized time complexity of O(1) for insertion and lookup operations.
- Set uses less memory than unordered_set to store the same number of elements.
- For a small number of elements, lookups in a set might be faster than lookups in an unordered_set.
- Even though many operations are faster in the average case for unordered_set, they are often guaranteed to have better worst case complexities for set (for example insert).
- That set sorts the elements is useful if you want to access them in order.
- You can lexicographically compare different sets with <, <=, > and >=. unordered_sets are not required to support these operations
Unordered Map (Hash Table) vs Map (Red Black Tree)